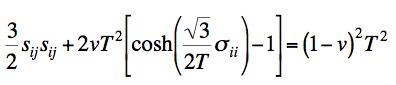Richard M. Christensen |
||
Damage
For present purposes it is helpful to consider three distinctly different types of damage in materials. First, there is the type of damage which is readily apparent before major yielding/failure. Secondly there can be apparent damage that occurs after the first major yielding, but during the continued loading phase. Thirdly there can be the type of barely observable, extremely small scale damage that occurs during loading but with no apparent consequences until abrupt final failure. These three cases, in different order, are exemplified by:
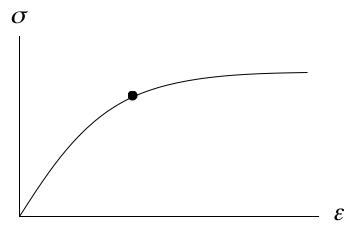
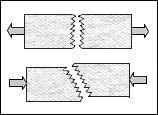
The three cases stated above will be expanded in the following discussion. Of course, these cases are somewhat idealized and actuality can sometimes show features composed of complex combination of these. Begin with the case of ductile metals. Ductile metals can fail in the mode called “ductile fracture”. The two words ductile and fracture in combination almost seem to pose a contradiction. Nevertheless they do describe a reality which is related to and is usually caused by damage. A schematic of a ductile metal stress strain curve is given by:
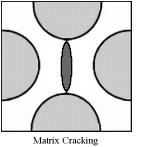
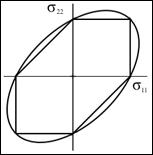
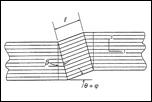
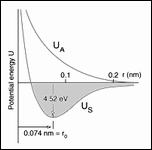
where v is the volume fraction of voids and T is the yield stress in uniaxial tension (and compression). For v=0 the form is that of the Mises criterion where sij is the deviatoric stress tensor. The presence of the voids as well as a possible mean normal stress effect, σii , acting with the voids, diminishes the yield stress from what it would be for a Mises criterion. Much more detailed forms have been devised using Gurson’s form as the starting point. These are as given by Tvergaard and by Needleman and by others. Reasonably general approaches are by Nahshon and Hutchinson1 and by Xue2 which contain references to the earlier works. In all of these works criteria are built into the procedure which specify the nucleation of the voids, the rate of growth of them, the interaction of them, and the possible coalescence of them to ultimately cascade into brittle fracture. These treatments also bring in the third invariant, not just the first two invariants as in the Gurson form. This circumstance is specified through a dependence upon the Lode angle in principle stress space which implies the existence and utilization of non-convex yield surfaces. All of the effects just described possibly leading to ductile fracture in ductile metals, involve inherently inhomogeneous effects and they dramatically illustrate the difficulties and complications that can follow from this type of void growth damage. In contrast to the above type of analysis, in the homogeneous material idealization of this website the point of major yielding in the above figure is interpreted as that of yield/failure. This approach then does not deal with the complication of whether the plastic flow is interrupted by fracture or not. The major load bearing function has already been sacrificed at the point of major yield, which is thus taken as that of effective failure. In further contrast to the above type of damage, fiber composite materials can undergo very extensive transverse cracking between fibers without showing much effect on the apparent stress strain behavior. This primarily occurs in polymeric matrix, carbon fiber systems, which are the most important type of high performance composite. However, the apparently benign nature of this type of damage can be deceiving. Transverse cracking within a lamia, which lamina is itself within a laminate, can provide the nucleation sites and energetics for delamination of the laminate. Delamination is the major weakness element in these materials The sequencing effect of these sources of degradation in these materials are called progressive damage and are treated herein. This website has two sections concerned with the failure of fiber composite materials. The first is at the aligned fiber, lamina level and represents the rather idealized failure type without damage at that level. Then, failure at the laminate level is treated and it involves the interactive effects of the ideal failure at the lamina level and the effect of progressive damage at the laminate level, ultimately resulting in the complete failure of the laminate. Yet another type(s) of damage must be involved under the cyclic loading conditions of fatigue. In this condition the damage is not readily discernable, at least not in a macroscopic sense. Yet the damage relentlessly grows and spreads until enough damage has accumulated to lead to sudden, often almost instantaneous failure. In materials with grains, this could be localized failure in the grain boundaries, while in fiber composites it could be debonding between the fiber and matrix phases. There are an unlimited number of different possible damage mechanisms for the different materials types. At first exposure it would seem almost impossible to theoretically characterize the growing state of fatigue damage along its transit toward failure. Nevertheless, out of necessity several approaches have been developed. Most of these are phenomenological in the sense that they are simply postulated forms that can be tested in different ways. A few approaches are physical in the sense that they represent a state of pre-existing cracks subject to kinetic growth control. It is this latter approach that will mainly be expanded in this website although representative cases of phenomenological forms will also be examined. It will be shown that the idealization of a single, non-interactive but growing crack is of limited value in fatigue problems and it is necessary to generalize to a related but more inclusive flaw growth methodology. This fatigue type of damage modeling is given under the heading of cumulative damage. It is found that a formalism can be taken that applies to either fatigue or creep rupture through suitable notational changes. The most basic problem associated with this area of study is to predict the lifetimes under variable amplitude loading conditions based upon knowledge of the data base of lifetimes under constant amplitude loading conditions. Other than the variation in the amplitude, all other characteristics such as frequency are held constant. In this manner the lifetime can then be predicted for any specified history of variable load amplitudes. These three major types of damage at least show the complexity of the microscale events leading up to failure. Failure at the atomic bond level or at the nanoscale or the microcscale do not necessarily imply or commit failure at the macroscale. Of course failure at the macroscale does imply all of the above, but failure at the macroscale itself has special meaning and restrictions. Nevertheless, the quantification of damage states can sometimes provide the link between all of these irreversible and deleterious subscale events and the final, ultimate failure of the material.
|
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
Recent Additons |
||||||||||||||||||||||||||||||||||||||||||||
Key Junctures |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
General Matters |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
Can Atomic/Nano Scale |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
Copyright© 2019 |
||||||||||||||||||||||||||||||||||||||||||||