|
Overview
- Three dimensional failure criteria are given for various materials classes. These include both isotropic and anisotropic material symmetries, and are applicable for macroscopic homogeneity. In the isotropic materials form, the properly calibrated failure criteria can distinguish ductile from brittle failure for specific stress states. Although most of the results are relevant to quasi-static failure, some are for time dependent failure conditions as well as for fatigue conditions.
Contents
- Purpose and Conditions - Attention is given to many failure related matters, but especially to the physical and mathematical basis for the failure criteria under examination.
- Yield and Failure Criteria for Isotropic Materials - Historical and modern failure criteria for isotropic materials are outlined and discussed. A recently developed yield and failure formalism is given which is completely calibrated by the two failure properties in uniaxial tension and compression. It necessarily involves an inherent transition from ductile to brittle failure mechanisms across the range of materials types.
Manuscripts of Published Papers
- Failure Criteria for Anisotropic Fiber Composite Materials - A physically based failure formulation is given for aligned fiber composite materials. Two coordinated failure criteria are derived, one for the fiber controlled mode and one for the matrix controlled mode. The targeted applications are to carbon fiber, polymeric matrix (or equivalent) types of systems.
- Cumulative Damage Leading to Fatigue and Creep Failure for General Materials - Four different cumulative damage models are compared. All four models are calibrated by constant amplitude failure data bases and do not contain any adjustable parameters. Only the flaw growth theory/model shows a consistent and realistic life prediction capability for variable amplitude conditions.
Manuscript of Published Paper
- Failure of Fiber Composite Laminates: Progressive Damage and Polynomial Invariants - Two distinctly different failure methods are given. The first is that of progressive damage where lamina level failure criteria are used to predict the sequence of damage/failures within the laminate. The second method is that of polynomial invariants which takes the scale of the laminate itself and its symmetry properties as the fundamental basis for failure characterization. The two methods are carefully and thoroughly compared.
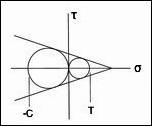
- Critical Experimental and Theoretical Tests for Failure Criteria - The evaluation procedure for isotropic material failure criteria involves assessing their theoretical basis followed by comparisons with critical data sets (ductile and brittle). All of the long standing commonly used failure forms are found to be fundamentally incapable of functioning as general three dimensional failure criteria. All but one (Mises) cannot even serve for just a single, restricted materials type. Only the recently developed, two property failure theory outlined in Section II correlates well with all the data cases and has complete generality, going from the ductile limit to the brittle limit. Some failure criteria for fiber composites are also evaluated.
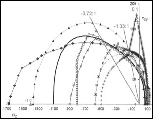
- The Ductile/Brittle Transition, Gaging Ductility Levels - Under the heading Organizing Principle the isotropic material failure criterion is put into the form that is best for examining ductility and brittleness matters. Starting with the ductile/brittle transition, a failure number index is derived that gages the level of ductility (and brittleness) in failure. The failure number, Fn, is expressed in terms of the uniaxial strength ratio, T/C, and the nondimensionalized first invariant of the stress state at failure. Many examples with detailed explanations are given.
- Fracture Mechanics - A sharply focused examination is taken of the two major failure disciplines: fracture mechanics and failure criteria. First, the historical development of the field of fracture mechanics is summarized. Then, typical but revealing examples of the use of each approach are given. Finally, the importance and usefulness of the two failure theories are assessed, both individually and relative to each other.
- Micromechanics Failure Analysis - The role of micromechanics in synthesizing macroscopic failure criteria is assessed. Micromechanics is seen as having a special capability beyond just that of predicting micron scale failure. Three examples are given that illustrate how particular failure modes at the micron scale bridge over to provide needed and sometimes critical information for macroscopic failure. Two of the examples are appropriate to carbon fiber composites, while the third one is for particulate composites.
- Defining Yield Stress and Failure Stress (Strength) - Historically there have been many different and confusing designations for the yield stress and strength. But for failure criteria purposes it is necessary to specify clear and rigorous definitions of these properties. The yield stress is determined to be given by the maximum of the second derivative of the stress strain curve. Since this is difficult to implement, an easy to use approximation to it is found. The strength property is determined to involve certain integrations over the stress strain curve, and it also is very easy to use with data.
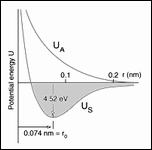
- Nanomechanics of Graphene - Graphene is the planar form of carbon atoms at only one atom of thickness. Its hexagonal coordination permits characterization of the corresponding in-plane isotropic, elastic properties. These properties are derived using a nondimensional nanoscale variable that differentiates between bond stretching and bond bending (distortion) effects. The resulting elastic properties and the ensuing failure consequences are found to have a profound dependence upon the nanoscale variable.
- Are the Elements Ductile or Brittle: A Nanoscale Evalutation – A failure mode analysis is given for those elements in the Periodic Table that form solids at ambient conditions. The nanoscale evaluation distinguishes between the bond bending and the bond stretching mechanisms of resistance and leads to a rank order list of the ductility’s for the most commonly considered elements. Some indications are also given to gauge the quantitative levels of ductility (or brittleness) for the elements.
- Probabilistic Failure and Probabilistic Life Prediction - The special characteristics of power law relations are used to derive the Weibull form of probability distribution functions, with no need to resort to the overly simplistic and misleading “chain of links” argument. Secondly, in a totally different direction, power law forms are used to derive the theory of kinetic crack growth culminating in macroscopic failure. Finally, the two formalisms are merged to yield a probabilistic treatment of materials failure. Critical tests of the overall theory are conducted using the largest database in existence for creep rupture failure (static fatigue).
- Completion and Closure on Failure Criteria for Unidirectional Fiber Composites - Building upon previous work in Sections III and IX the failure criterion for unidirectional fiber composites is examined using a sensitivity analysis as applied to its transverse, matrix controlled failure properties. A new and general relationship is found between these three properties thereby reducing the number of independent properties needed to calibrate the theory to five. A broad but detailed evaluation of the resulting failure criterion is given. The results are conclusive and final.
- Failure Mechanics: The Coordination Between Elasticity Theory and Failure Theory - Failure mechanics is comprised of the failure theory for homogeneous and isotropic materials along with all of its implications and applications. The present failure theory is found to have an intimate connection with elasticity behavior even though plasticity may also transpire. This becomes apparent and useful when the classical theory of elasticity is renormalized to give a simpler and more transparent (but still exact) formalism. The connection or coordination between elasticity and failure then explicitly occurs through the use of the renormalized Poisson’s ratio to characterize the ductility of failure. With this unification of failure theory and elasticity theory, failure mechanics can be appraised in its complementary relationship to fracture mechanics and to all of the other historical mechanics related disciplines.
- Failure Mechanics: The Central and Decisive Role of Graphene in Defining the Elastic and Failure Properties - Continuing from Part I, [1], the relationship between elastic energy and failure specification is further developed. Part I established the coordination of failure theory with elasticity theory, but subject to one overriding assumption: that the values of the involved Poisson’s ratios always be non-negative. The present work derives the physical proof that, contrary to fairly common belief, Poisson’s ratio must always be non-negative. It can never be negative for homogeneous and isotropic materials. This is accomplished by first probing the reduced two dimensional elasticity problem appropriate to graphene, then generalizing to three dimensional conditions. The nanomechanics analysis of graphene provides the key to the entire development.
- Why Carbon Based Materials are so Exceptional and Vital - The element carbon in its many different and distinctive materials forms usually has superior properties compared with other materials. The mechanical properties of stiffness and strength for the different forms of carbon are examined. Ductility is also considered. The materials forms include diamond, graphene, graphite, fullerenes, nanotubes, carbon fibers and carbon fiber/ polymeric matrix composites. The range of behaviors are surveyed and in some critical cases studied in closest detail, including at the nanoscale.
- A New Theory of Strain Hardening and its Consequences for Yield Stress and Failure Stress - A new theory of strain hardening is developed. Important in its own right, the strain hardening solution is also of decisive use in rigorously defining the historically broad concepts of yield stress and failure stress. Under ideal conditions yield stress is found to represent a 3rd order transition. Failure stress is an explicit “failure of function” criterion rather than just being the primitive notion of breaking into pieces. Computational extensions and opportunities are discussed.
- Evaluation of Ductile/Brittle Failure Theory, Derivation of the Ductile/Brittle Transition Temperature - A recently developed ductile/brittle theory of materials failure is evaluated. The failure theory applies to all homogeneous and isotropic materials. The determination of the ductile/brittle transition is an integral and essential part of the failure theory. The evaluation process emphasizes and examines all aspects of the ductile versus the brittle nature of failure, including the ductile limit and the brittle limit of materials types. The failure theory is proven to be extraordinarily versatile and comprehensive. It even allows derivation of the associated ductile/brittle transition temperature. This too applies to all homogeneous and isotropic materials, not just to some sub-class of materials types. This evaluation program completes the development of the failure theory.
- First Ply Failure As Determined By The Most Rigorous (Yet Simplest) Fiber Composites Failure Criterion And Failure Theory - After reviewing the World Wide Failure Exercise, WWFE, the case of the failure of isotropic materials is taken up as necessary background for the main interest in fiber composites failure. Then using the same method as with the isotropic materials case, the failure criteria are given for highly anisotropic, unidirectional fiber composite materials. The failure criteria are calibrated by the fiber direction tensile and compressive strengths, the transverse direction tensile and compressive strengths and the axial shear strength. These five strength properties give the full and complete failure specification. No empirical and adjustable failure parameters are involved or allowed by the derivation. This failure theory is then used to give the first ply failure characterization for a quasi-isotropic laminate composed of unidirectional lamina.
- Failure Theory/Failure Criteria For Fiber Composite Laminates - Failure criteria are derived for the case of a quasi-isotropic laminate and for the more general case of orthotropic laminates. The former requires two calibrating failure properties obtained directly from laminate testing and the latter requires five standard experimental measurements for its calibration. Then the quasi-isotropic failure theory is taken much further, also admitting full calibration by only the two composites tow failure properties, the associated tensile and compressive strengths. The theoretically predicted failure envelope for the quasi-isotropic laminate is favorably compared with some comprehensive testing data. As a related matter, the general failure criteria for unidirectional fiber composites are also reviewed.
- Lamination Theory for the Strength of Fiber Composite Materials - Building upon previous work for the failure of quasi-isotropic fiber composite laminates, the much more difficult and more important general case of orthotropic laminates is now taken up. The full and complete failure criterion is derived for fiber dominated, general 0, 90, ±45 degree laminated materials, with the relative volume fractions to be specified for each direction. Quasi-isotropy is a special case of the orthotropic formalism and the general orthotropic results are just as rigorous as the previous specialized quasi-isotropic results. The orthotropic failure criterion results are of direct and immediate relevance in composites materials applications using advanced numerical/digital methods
.
- Perspective On Materials Failure Theory and Applications - The history of developing failure criteria is briefly examined. The cumulative result is found to be completely unsatisfactory and extremely misleading, to the point of crisis. A new and rationally different approach to failure theory formulation is outlined and fully documented. After summarizing recent research progress, a program for the recovery and revitalization of the field is given.
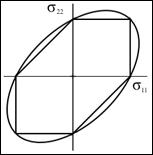
- Materials Failure Theory, Strain Energy, and Principal Stresses Eigenvalue Problem - The three sub-disciplines of principal stresses, strain energy, and failure theory are shown to depend upon four basic invariants. These four invariants are derived from the eigenvalue problem of the principal stress formulation. Thus, the most basic form of all the three areas is that of the eigenvalue problem for the principal stresses. The proper forms for the strain energy and the failure problem follow from the eigenvalue problem, both being appropriate to isotropic materials. After further showing the specific relationship between the failure theory and the strain energy, some implications of the failure theory are examined.
- The Ductility Number Nd Provides A Rigorous Measure For The Ductility Of Materials Failure - The recently developed theory for isotropic materials failure is briefly outlined. The many steps and stages of the verification process for the theory are fully documented so that it can be used with assurance in a wide variety of directions. Then the failure theory is used to develop a new measure or index for the degree of ductility of materials failure in any state of stress. This new failure property is named the ductility number, Nd. It is rigorously derived, intuitively compatible, and very easy to use. Applications and interpretations of Nd are given.
- The Proof Of The Splitting Mode Of Compressive Brittle Failure And Integration With General Failure Theory - The problem of special interest is the nature of the mode of failure in uniaxial compression at the brittle limit. This problem is known by observation to undergo a splitting mode of failure. The present work gives a full theoretical treatment and proof for this mode of failure. The general failure theory of Christensen for isotropic materials provides the basis for the derivation. The solution demonstrates the depth of technical capability that is required from the failure theory in order to treat such a classically difficult problem.
|
|
|