Richard M. Christensen |
||
|
||||
Recent Additons |
||||||
Key Junctures |
||
 |
||||
General Matters |
||||
 |
||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
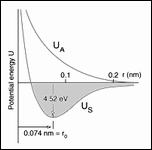
Can Atomic/Nano Scale |
||||||||
 |
||||||
 |
||||||
 |
||||||
 |
||||||
 |
||||||||
 |
||||||||
 |
||||||
 |
||||||
 |
||||||||
 |
||||||||
 |
||||||
Copyright© 2019 |
||||||
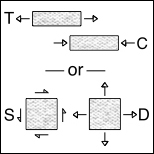
Which is Fundamental: T&C or S&D
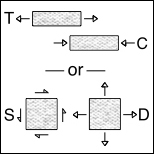 If, as argued here, there exists a comprehensive theory of failure for isotropic materials, then the most favorable situation would be that of two calibrating failure properties in coordination with the two elastic properties of physical/mechanical behavior. The most common sets of elastic properties are either μ and k or E and ν. The present theory of isotropic material failure employs the uniaxial strengths T and C as associated with E and ν. But this suggests that one could as well take the shear strength, S, and the positive dilatational strength, D, as associated with μ and k. This alternative approach is a matter worth examining.
If, as argued here, there exists a comprehensive theory of failure for isotropic materials, then the most favorable situation would be that of two calibrating failure properties in coordination with the two elastic properties of physical/mechanical behavior. The most common sets of elastic properties are either μ and k or E and ν. The present theory of isotropic material failure employs the uniaxial strengths T and C as associated with E and ν. But this suggests that one could as well take the shear strength, S, and the positive dilatational strength, D, as associated with μ and k. This alternative approach is a matter worth examining.
The fact that all stress states can be built up from the superpositions of states of distortion and dilatation could lead one to suspect that S and D may be more fundamental than T and C. Furthermore, this superposition capability suggests (but does not prove) that two failure properties should indeed suffice for describing all isotropic material failures. Proof can only follow from experimental verification
Next the failure criterion used here and based upon T and C will be recalled. Then it will be expressed in terms of S and D to see whether the formulation becomes more clarified, less clarified, or completely opaque compare with that using T and C.
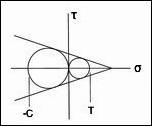
The failure criterion (criteria) developed and used here is given by
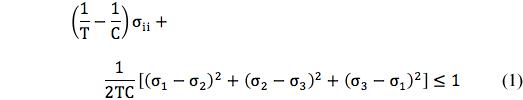
with the competitive fracture criterion as
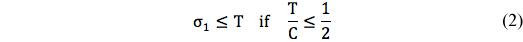
where σ1 is the largest principal stress.
Take S as the failure stress in shear and D as the failure stress in positive dilatation. Henceforth D will be referred to as dilation failure. Then (1) becomes
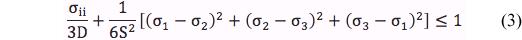
where
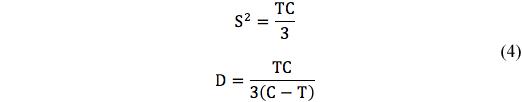
The fracture criterion (2) becomes
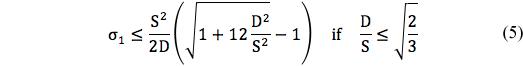
The first observation to be made is that the fracture criterion (2) when expressed in terms of S and D, (5), is completely devoid of physical interpretation. If the comparison of using T and C versus S and D only involved the polynomial invariants criterion (1) or (4) there would be little to choose between them. But the real problem is with the fracture criterion. The fracture criterion is very important, and not just in applications. It admits the limiting case of perfectly brittle behavior, without which there is no closure to the theory, no actual assurance of generality.
Consider the relationships of T and C with E and ν and correspondingly that of S and D with μ and k. From an operational, linear elasticity point of view, knowing the properties μ and k is absolutely equivalent to knowing E and ν. But from a physical point of view and especially with implications for failure, the two sets of elastic properties may or may not be entirely equivalent.
The possibly deeper meaning of E and ν versus μ and k is that the scale of the load bearing resistance or capability in the one case is concentrated into one property, E, rather than into two properties, μ and k. The Poisson’s ratio ν serves a completely different role as will be mentioned later.
The limiting cases for the two forms are specified by

Some formulations with μ and k involve indeterminacies and discontinuities whereas those with E and ν usually do not. A non-trivial example will be given that illustrates this.
An evaluation example is needed that not only involves stress and strain under elasticity conditions, but also the example should have implications or significance for failure behavior. Since isotropy is being considered here it must comply with that as well. The ideal example turns out go be that for the effective behavior of an elastic medium having a randomly oriented and distributed array of cracks.
In a major work, Budiansky and O’Connell [1] gave the solution for the effective properties of an isotropic, elastic material containing a damage pattern of randomly oriented cracks. This problem and solution is ideal for present purposes. It brings in elastic properties, damage, and failure significance. The only potential problem with using this work is that some have questioned the meaning of its prediction of material collapse at a value of ε = 9/16 where ε is the crack density variable of circular cracks.
This result for material collapse is sometimes criticized as being arbitrary, or arbitrarily small. So before using the results of this work, its validity will be reinforced by showing the logic and consistency of its prediction of the loss of material integrity at ε = 9/16.
For circular cracks the crack density is defined as
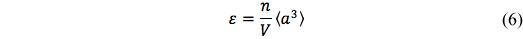
where “a” is the radius of the randomly distributed cracks with <a3> being an average, and n the number of cracks existing within the volume V. For extension to more general cracks of convex shape the crack density is taken as
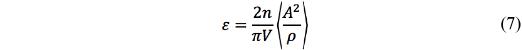
where A is the crack area and ρ its perimeter.
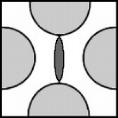
To verify the prediction of material collapse at ε = 9/16, consider different possible crack patterns at material collapse. The faces of some of the platonic solids will be taken to represent the fully developed crack patterns at collapse. The only platonic solids or combination of platonic solids that pack perfectly in 3-space are the cube and a 2:1 combination of tetrahedra and octahedra.
Dodecahedra do not pack in 3-space although they come fairly close to doing so. The dihedral angle for a dodecahedron is θ = 116.57°. If this angle were 120° there would be perfect packing. As an estimate for that obtained from the dodecahedron, take the number of sides of the single cell as 12, recognizing that if there were perfect packing the appropriate number would be 6 since each face would be shared with the neighboring cell. This then recognizes the imperfect packing, leaving a small amount of material as being left over to form a “skeleton” of remaining connected material at or near collapse. In solving for ε for the case of the dodecahedron the volume will be taken as that of the dodecahedron itself. Thus this estimate for ε can be viewed as an upper bound.
The respective values of ε for these three cellular cases of fully developed crack patterns are determined from (7) to be given by:

Self Consistent ε = 9/16 = 0.5625
In terms of the crack pattern symmetries, the first two cases have cubic symmetry while the third is isotropic. Based on these results it is completely reasonable and rational to expect that ε = 9/16 gives the minimum crack density value for material collapse due to an isotropic pattern of cracks and correspondingly for a random distribution of cracks.
As a consequence of the above comparison, the results of Budiansky and O’Connell will be taken as the rigorous solution of the problem. These results will now be used for present purposes. As an aside, the Generalized Self Consistent Method is the preferred effective properties approach for two phase media, while the Self Consistent Method is the preferred approach for single phase media containing cracks or grain boundaries. It is the latter method that was used by Budiansky and O’Connell.
The notation of Budiansky and O’Connell takes Ec , νc , μc , and kc as the effective elastic properties of the medium containing the cracks. The same symbols without the subscripts are the properties of the uncracked material.
Of the four properties Ec , νc , μc , and kc it is only νc as a function of ε that can be determined as an uncoupled equation apart from any other of the properties. Once νc is found then the other three properties can be determined as functions of ε. In general, νc as a function of ε and ν is a cubic equation but its analytical solution can be found in the special case of ν = 1/2. This solution for circular cracks is given by
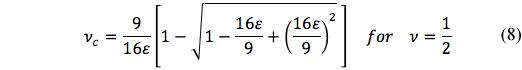
Eq. (8) is indeterminate at ε=0 but it can easily be evaluated and gives the proper result of νc=1/2 at ε=0. Knowing νc , the other properties can be found, such as for Ec , from
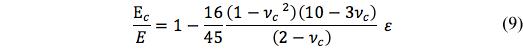
Similar forms are found for μc and kc.
The general solutions for Ec , νc , μc , and kc have the following characteristics. At ν = 0
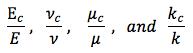
all are the same linear function of ε going from the value of 1 at ε = 0 to the value of 0 at ε = 9/16. They gradually deviate from linearity as ν is increased from zero, going to maximum deviations at ν = 1/2. Thus it suffices to examine the cases at ν = 1/2 to see the maximum deviations from linearity.
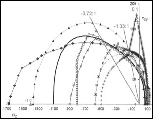
The properties behaviors at ν = 1/2 are as shown in Fig. 1.
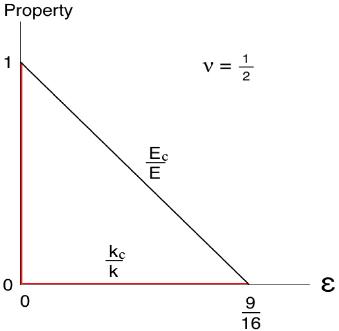
Fig. 1 Properties variations as functions of crack density
The slight deviation of Ec/E from linearity will be specified below, kc/k is discontinuous with ε. The variation of νc/ν in Fig. 1 is a little above that for Ec/E, necessarily being concave down with the same end points. And that for μc/μ is considerably above that for νc/ν, also concave down. The deviations from linearity in plots of the type in Fig. 1 can be found as follows.
The mid-points of the variations, in Fig. 1, are at ε = 9/32. At this mid-value of ε and for this worst case of ν = 1/2 the properties values are found to be
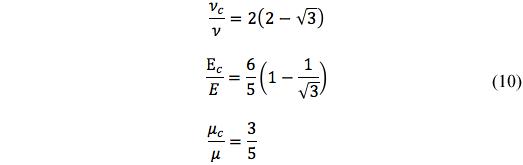
Thus the maximum deviations from linearity are found to be
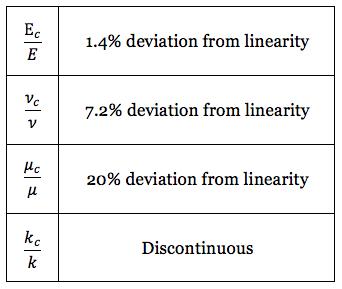
The result that kc be discontinuous when ν = 1/2 can easily be reasoned as being physically required. Recognizing the intimate relationship of the effective properties to fracture mechanics it is reasonable to expect that the dilation failure property, D, would also suffer a discontinuous or nearly discontinuous behavior with variations of ε.
It is seen that Ec and νc have a special behavior not shared by μc and kc. In other sections it has been discussed that failure criteria can be interpreted as the tensorial description of the termination of the elastic range of behavior. In this sense there is an association of elastic properties and failure properties. Plastic flow behavior does not contradict this, it just describes a more complex transition from elastic behavior to failure. In relation to this, the behaviors of Ec and νc , as found by Budiansky and O’Connell over the full range of crack densities, show vastly more regularity and smoothness than do μc and kc. Furthermore, the difference in behavior in this problem between Ec and νc is minor, while the disparity between μc and kc behaviors is huge.
The special behavior of the Poisson’s ratio ν is quite interesting. Although T and C relate most directly to E itself, ν also may have some meaning for failure behavior. Most but not all engineering materials have Poisson’s ratios that fall within 1/5 ≤ ν ≤ 1/2. Nothing of this type can be said for μ and k except by inference from ν. Further, Poisson’s ratios give some indication of a materials failure type. Within the range stated above, the lower Poisson’s ratios relate to brittle failure while the mid range and some higher ones relate to ductile failure usually.
In conclusion of these results and observations, the elastic properties E and ν and their failure conjugates T and C are much more likely to be the fundamental continuum mechanics pairings than are the elastic properties μ and k and their failure conjugates S and D. It may also be noted that as a practical expedient, the uniaxial strengths, T and C, are enormously easier to experimentally determine with reliability than are the shear and dilation strengths, S and D. Agreeably then the likely fundamental forms and the practical approach for failure properties determination are in harmony, not in conflict.
Reference
Budiansky, B. and O’Connell, R. J., 1976, “Elastic Moduli of a Cracked Solid”, Int. J. Solids Structures, 12, 81-97.



